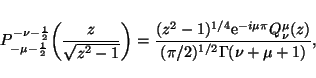 |
(28) |
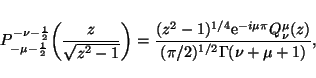 |
(28) |
and,
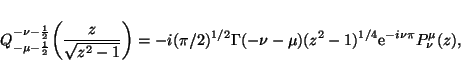 |
(29) |
which are valid only for
![]() (since the
Legendre function of the second kind becomes discontinuous on the cut)
and for all complex
(since the
Legendre function of the second kind becomes discontinuous on the cut)
and for all complex ![]() and
and ![]() except when
except when
![]() since the Gamma function has poles along the negative real axis.
By combining eqs. (28) and (29) with eqs. (20)--(23) along with the
negative argument condition for Gamma functions [eq. (6.1.17) of Abramowitz
& Stegun (1965)], namely,
since the Gamma function has poles along the negative real axis.
By combining eqs. (28) and (29) with eqs. (20)--(23) along with the
negative argument condition for Gamma functions [eq. (6.1.17) of Abramowitz
& Stegun (1965)], namely,
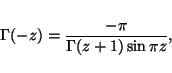 |
(30) |
![\begin{displaymath}P_{\nu-\frac{1}{2}}^\mu(z)=
\frac{\sqrt{2}\ \Gamma(\mu-\nu+\f...
...-\frac{1}{2}}^\nu
\biggl(\frac{z}{\sqrt{z^2-1}}\biggr)\Biggr],
\end{displaymath}](an/img67.gif) |
(31) |
which is equivalent to,
![\begin{displaymath}Q_{\nu-\frac{1}{2}}^\mu(z)=
\frac{\mathrm{e}^{i\mu\pi}\Gamma(...
...\frac{1}{2}}^\nu
\biggl(\frac{z}{\sqrt{z^2-1}}\biggr)
\Biggr].
\end{displaymath}](an/img68.gif) |
(32) |
Now, we substitute ![]() and
and ![]() (with m and n being
positive integers) in (28) and (29) in order to derive the Whipple formulae
for associated toroidal functions
(with m and n being
positive integers) in (28) and (29) in order to derive the Whipple formulae
for associated toroidal functions
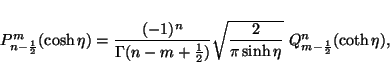 |
(33) |
which is equivalent to,
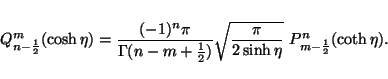 |
(34) |
These last two expressions allow us to express toroidal functions
of a certain kind (first or second, respectively) with argument hyperbolic
cosine, as a direct proportionality in terms of the toroidal function of the
other kind (second or first, respectively) with argument hyperbolic
cotangent. The Whipple formulae may also be expressed as follows:
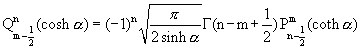 ,
,  ,
, 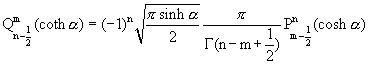 , and,
, and, 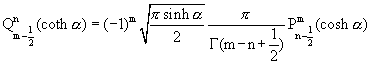 .
.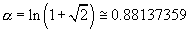 .
. 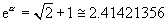 ,
, 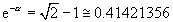 .
. 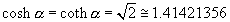 .
. 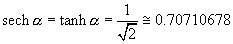 .
.  .
.