CLICK TEXT TO READ PDF COPY OF PAPER
Here we present, as examples, the negative degree condition for
associated Legendre functions of the first
kind (cf., eq. [8.2.1] in Abramowitz & Stegun 1965),
 |
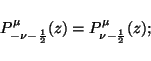(20) |
the negative degree condition for associated Legendre functions
of the second kind (cf., eq. [8.2.2] in Abramowitz & Stegun 1965),
![\begin{displaymath}Q_{-\nu-\frac{1}{2}}^\mu(z) = \frac{1}{\cos\pi(\nu-\mu)}
\big...
...rm{e}^{i\mu\pi}\sin\nu\pi\ P_{\nu-\frac{1}{2}}^\mu(z)
\biggr];
\end{displaymath}](img51.gif) |
(21) |
the negative order condition for associate Legendre functions
of the first kind (cf., eq. [8.2.5] in Abramowitz & Stegun 1965),
![\begin{displaymath}P_{\nu-\frac{1}{2}}^{-\mu}(z) =
\frac{\Gamma(\nu-\mu+\frac{1...
...m{e}^{-i\mu\pi}
\sin\mu\pi\ Q_{\nu-\frac{1}{2}}^\mu(z)\biggr];
\end{displaymath}](img52.gif) |
(22) |
and, finally, the negative order condition for associate
Legendre functions
of the second kind (cf., eq. [8.2.6] in Abramowitz & Stegun 1965),
 |
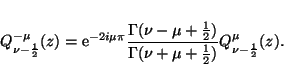(23) |
For toroidal functions with 
and 
being positive integers,
we derive from eqs. (20)--(23),
 |
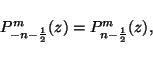(24) |
 |
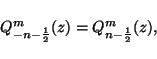(25) |
 |
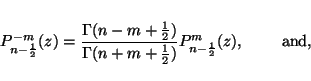(26) |
 |
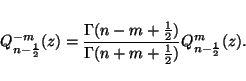(27) |
It can also be shown with very little algebra that both equations
(26) and (27) are invariant under index interchange.
