Next: Rotationally Invariant Coordinate Systems Up: Developments in Determining the Previous: Developments in Determining the

associated Legendre functions : Cohl et. al. (2000)
New addition theorem for spherical coordinates : Cohl et. al. (2001)
Solar White Light Flares : Neidig et. al. (1993)

1997 - Cohl, H. S., Xian-He Sun and J. E. Tohline
"Parallel Implementation of a Data-Transpose Technique for the Solution of Poisson's Equation in Cylindrical Coordinates"
Proceedings of the 8th SIAM Conference on Parallel Processing for Scientific Computing, Minneapolis, Minnesota, March.
1999a - Cohl, H. S.
"On the numerical solution of the cylindrical Poisson equation for isolated self-gravitating systems"
The Louisiana State University and Agricultural and Mechanical College, 122 pages
1999b - Cohl, H. S. and J. E. Tohline
"A Compact Cylindrical Green's Function Expansion for the Solution of Potential Problems"
The Astrophysical Journal, 527, 86-101.
2000 - Cohl, H. S., J. E. Tohline, A. R. P. Rau, H. M. Srivastava
"Developments in determining the gravitational potential using toroidal functions"
Astronomische Nachrichten, 321, 5/6, 363-372.
2001 - Cohl, H. S., Rau, A. R. P., Tohline, J. E., Browne, D. A., Cazes, J. E. and Barnes, E. I.
"Useful alternative to the multipole expansion of 1/r potentials"
Physical Review A: Atomic and Molecular Physics and Dynamics, 64, 5, 52509.
2002 - Cohl, H. S.
"Portent of Heine's Reciprocal Square Root Identity"
Proceedings of the 3D Stellar Evolution Workshop, ed. R. Cavallo, S. Keller, S. Turcotte, Livermore, California

Introduction

CLICK TEXT TO READ PDF COPY OF PAPER

There are many different types of systems in the universe whose structural and dynamical properties are governed by self-gravity. Furthermore, the very existence of atoms is a direct consequence of the electromagnetic attraction between negatively charged electrons and positively charged, centrally concentrated, nuclei. In order to determine the fields associated with general nonaxisymmetric mass/charge distributions, $\rho({\bf x},t),$ accurate means of computing the Newtonian/Coulomb potentials, $\Phi({\bf x},t),$ are needed.

In an astrophysical context (cf., §2.1 in Binney & Tremaine 1987), the Newtonian potential is determined by solving the appropriate boundary-value problem that is given by the three-variable Poisson equation,

$\begin{displaymath}\nabla^2 \Phi({\bf x}) = 4\pi\mathrm{G}\rho({\bf x}), \end{displaymath}$

(1)

where $\nabla^2$ is the Laplacian, and $\mathrm{G}\simeq6.6742\times 10^{-8}\ \mathrm{cm^3\ g^{-1}\ sec^{-2}}$ is the gravitational constant. Exterior to an isolated mass distribution, physically correct boundary conditions may be imposed on Poisson's equation through the following integral formulation of the potential problem,

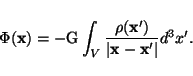$\begin{displaymath}\Phi({\bf x}) = -\mathrm{G}\int_V \frac{\rho({\bf x^\prime})}{\vert{\bf x}-{\bf x^\prime}\vert} d^3x^\prime. \end{displaymath}$

(2)

Due to the long-range nature of the Newtonian/Coulomb interaction, a physically correct solution of Poisson's equation and, hence, an accurate determination of the potential ``interior'' to the boundary can be highly boundary value dependent. If inaccurate potential values are given on the boundary, the interior solution will reflect these defects.

In numerical simulations of astrophysical systems, a standard procedure for determining the value of the gravitational potential along the boundary of a computational mesh has been the multipole method. In this method, an approximate solution to equation (2) is obtained by summing up higher and higher order spherical multipole moments (monopole, dipole, quadrupole, etc.) of the mass distribution. The multipole moments themselves are normally cast in terms of two quantum numbers -- one meridional $\ell,$ and one azimuthal m -- and for practical reasons the series summation is truncated at a finite value of $\ell$ and m. An alternative to the standard multipole expansion has been given by Cohl & Tohline (1999) in terms of a single sum over the azimuthal quantum number m. This new expression yields the pure azimuthal mode contribution to the Newtonian potential. In terms of the standard multipole description, this new expansion is equivalent to completing the infinite sum over the quantum number $\ell$ for each given value of the quantum number m (Cohl et al. 2000). It is now clear to us that this new expansion can be extended to every rotationally invariant coordinate system which separates the three-variable Laplace equation.

In §2 we describe the rotationally invariant coordinate systems which separate Laplace's equation and briefly describe some of the properties of these systems related to the double summation/integration expressions for the reciprocal distance between two points (hereafter, Green's function for Laplace's equation, or just Green's function) in these coordinate systems. In §3 we describe the key expressions for the Green's function in circular cylindrical coordinates, and show how these expressions are consistent with an azimuthal Fourier series expansion for the Green's function whose coefficients are given in terms of toroidal functions. In §4 we describe some of the highly symmetric properties of toroidal functions, such as their behavior for negative degree and order. We also present toroidal function implications of the Whipple formulae for associated Legendre functions. Using these Whipple formulae for toroidal functions, we then obtain a new expansion which is shown to be equivalent to the expansion given in Cohl & Tohline (1999). In §5 we briefly summarize several key mathematical implications of these expansions as they apply to prolate spheroidal, oblate spheroidal, and, parabolic coordinates. In §6 we present some key mathematical implications of these expansions as they apply to bispherical, and toroidal coordinates. All of the coordinate systems presented in §§5 and 6 have known double integration/summation expansions for the Green's function and therefore can be easily related to these new alternative expansions. A detailed treatment in spherical coordinates is being presented elsewhere (Cohl et al. 2000). The mathematical relations we derive below are either in the form of an infinite integral or an infinite series expansion over the set of basis functions which separate Laplace's equation.

Since toroidal functions can be used to unify all of the rotationally invariant coordinate systems which separate Laplace's equation, we suspect that they represent a basis set that is better suited for general studies of nonaxisymmetric mass/charge distributions than, for example, spherical harmonics. It is with this in mind, that the relations in this paper are presented for use in numerical and analytical solutions to any theoretical physics problem which requires accurate evaluation of the gravitational and/or Coulomb potential.

Next: Rotationally Invariant Coordinate Systems Up: Developments in Determining the Previous: Developments in Determining the

Howard S. Cohl
2000-10-05

Cohl, H. S., J. E. Tohline, A. R. P. Rau, H. M. Srivastava (2000)

Astronomische Nachrichten, 321, 5/6, 363-372.

"Developments in determining the gravitational potential using toroidal functions."

Site at a Glance: