Please feel free to enjoy my contributions to these interesting fields:

Numerical solution for 3D Poisson equation in circular cylindrical coordinates : Cohl et. al. ( 1997, 1999a)
Green's function for 3D Laplace equation : Cohl et. al. ( 1999a, 1999b, 2000, 2001, 2002)
Gravitational potential : Cohl et. al. ( 1999a, 1999b, 2000, 2001, 2002)
Quadrics & cyclides : Cohl et. al. ( 1999a, 1999b, 2000, 2001, 2002)
Heine identity : Cohl et. al. ( 1999a, 1999b, 2000, 2001, 2002)
Cylindrical, toroidal, oblate and prolate spheroidal, parabolic, bispherical coordinate systems : Cohl et. al. (1999a, 2000)
New addition theorems for rotationally invariant coordinate systems which R-separate 3D Laplace equation: Cohl et. al. (1999a, 2000)
3D biharmonic, 3D triharmonic, and 3D higher harmonic Green's functions : Cohl (2002)
Spherical coordinate system : Cohl et. al. (2001)
Coulomb direct (classical) and exchange (quantum) integrals/interactions : Cohl et. al. (2001)
Two-electron interactions : Cohl et. al. (2001)
Spherical azimuthal and separation angle Fourier expansions : Cohl et. al. (2001)
Magnetic field of an infinitesimally thin circular current loop : Cohl & Tohline (1999)
Symmetry properties of associated Legendre/toroidal functions : Cohl et. al. (2000)
Whipple formulae for toroidal/associated Legendre functions : Cohl et. al. (2000)
New addition theorem for spherical coordinates : Cohl et. al. (2001)
Solar White Light Flares : Neidig et. al. (1993)

1997 - Cohl, H. S., Xian-He Sun and J. E. Tohline
"Parallel Implementation of a Data-Transpose Technique for the Solution of Poisson's Equation in Cylindrical Coordinates"
Proceedings of the 8th SIAM Conference on Parallel Processing for Scientific Computing, Minneapolis, Minnesota, March.
1999a - Cohl, H. S.
"On the numerical solution of the cylindrical Poisson equation for isolated self-gravitating systems"
The Louisiana State University and Agricultural and Mechanical College, 122 pages
1999b - Cohl, H. S. and J. E. Tohline
"A Compact Cylindrical Green's Function Expansion for the Solution of Potential Problems"
The Astrophysical Journal, 527, 86-101.
2000 - Cohl, H. S., J. E. Tohline, A. R. P. Rau, H. M. Srivastava
"Developments in determining the gravitational potential using toroidal functions"
Astronomische Nachrichten, 321, 5/6, 363-372.
2001 - Cohl, H. S., Rau, A. R. P., Tohline, J. E., Browne, D. A., Cazes, J. E. and Barnes, E. I.
"Useful alternative to the multipole expansion of 1/r potentials"
Physical Review A: Atomic and Molecular Physics and Dynamics, 64, 5, 52509.
2002 - Cohl, H. S.
"Portent of Heine's Reciprocal Square Root Identity"
Proceedings of the 3D Stellar Evolution Workshop, ed. R. Cavallo, S. Keller, S. Turcotte, Livermore, California


Rotationally Invariant Coordinate Systems which Separate Laplace's Equation

CLICK TEXT TO READ PDF COPY OF PAPER

It is well-known that Laplace's equation

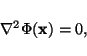$$\nabla^2 \Phi({\bf x}) = 0,$$ (3)

admits a number of different separable solutions for the function $\Phi({\bf x})$ that are given in terms of products of known special functions whose arguments, in turn, are given in terms a triply-orthogonal set of curvilinear coordinates $\{\xi_1,\xi_2,\xi_3\}$ (Bôcher 1894; §10.3 in Morse & Feshbach 1953; §3.6 in Miller 1977). These solutions can be classified as being either simply separable, $\Phi({\bf x})=\Xi_1(\xi_1)\Xi_2(\xi_2)\Xi_3(\xi_3),$ or ${\cal R}$-separable $\Phi({\bf x})=[\ \!\!\Xi_1(\xi_1)\ \Xi_2(\xi_2)\ \Xi_3(\xi_3)]/{\cal R} (\xi_1,\xi_2,\xi_3)$, where the modulation factor ${\cal R}(\xi_1,\xi_2,\xi_3)$ (§5.1 in Morse & Feshbach 1953) is a scalar function that has a unique specification for each coordinate system. The simply separable coordinate systems can be geometrically characterized by surfaces that are quadric (second-order); whereas the ${\cal R}$-separable coordinate systems are characterized by surfaces which are cyclidic (fourth-order). Using a Lie group theoretic approach Miller (1977) has demonstrated that there are precisely seventeen conformally independent separable coordinate systems that are either simply separable or ${\cal R}$-separable for Laplace's equation. In general, these separable Laplace systems can be broken up into three classes: a cylindrical class (i.e., invariant under vertical translations), a rotational class (i.e., invariant under rotations about the z-axis), and a more general class.

Here we will focus on the rotational class of Laplace systems, that is, those systems that correspond to the diagonalization of the z-component of the angular momentum operator

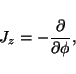$$J_z = -\frac{\partial}{\partial \phi},$$ (4)

where $\phi$ is the azimuthal coordinate. These coordinate systems share the special property that their eigenfunctions take the form

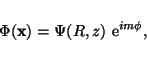$$\Phi({\bf x}) = \Psi(R,z)\ \mathrm{e}^{im\phi},$$ (5)

where R represents the distance from the z-axis (i.e., the cylindrical radius), z is the vertical height, and

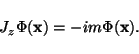$$J_z \Phi({\bf x}) = -im\Phi({\bf x}).$$ (6)

If we substitute (5) into Laplace's equation and factor out $\mathrm{e}^{im\phi}$, we obtain a differential equation for $\Psi$, which is the foundation of generalized axisymmetric potential theory; written in cylindrical coordinates, for example, this key equation takes the form,

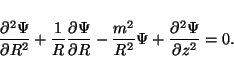$$\frac{\partial^2\Psi}{\partial R^2} + \frac{1}{R}\frac{\parti... ...frac{m^2}{R^2}\Psi + \frac{\partial^2 \Psi}{\partial z^2} = 0.$$ (7)

Miller (1977) also has shown that there are precisely nine conformally independent rotational Laplace systems. Five of these coordinate systems (cylindrical, spherical, prolate spheroidal, oblate spheroidal, and, parabolic) are quadric and simply separable for Laplace's equation; the remaining four (one of which is toroidal) are cyclidic and ${\cal R}-$separable for Laplace's equation. Moon & Spencer (1961b, §IV) have tabulated ten fourth-order rotational Laplace systems. Consulting Miller's (1977) study, we know that under any conformal symmetry of the Laplace equation, an ${\cal R}-$separable coordinate system can be mapped to another ${\cal R}-$separable coordinate system. Therefore, one might question whether all of Moon & Spencer's (1961b) rotational Laplace systems have unique double summation/integration Green's function expansions, and how many such coordinate systems exist.

Discussions of the double summation/integration expressions for the Green's function expansions (Jackson 1975, Chapter 3; Morse & Feshbach 1953, Chapter 10) for cylindrical (Cohl & Tohline 1999; see also §3 below) and spherical coordinates (Cohl et al. 2000) is abundant in the literature. Double summation/integration expressions for the Green's function for the three remaining quadric rotational Laplace systems (oblate spheroidal, prolate spheroidal, and, parabolic coordinates) also have been previously presented in the literature (Hobson 1931, §§245 and 251; Morse & Feshbach 1953, §10.3) and therefore present themselves easily for comparison. As for the cyclidic coordinate systems, the double summation expressions for the Green's functions in toroidal and bispherical coordinates have been developed (cf., Morse & Feshbach 1953, §10.3; Hobson 1931, §258; see also §6.2 below), but we have been unable to locate the double summation/integration Green's function expansions for the other rotational cyclidic Laplace systems. The three remaining conformally unique cyclidic rotational Laplace systems have ${\cal R}-$separable transcendental function solutions to Laplace's equation that are in the form of Lamé functions and Jacobi elliptic functions. We anticipate discussing these less well known cyclidic coordinate systems, as well as the remaining rotational Laplace coordinate systems presented in Moon & Spencer (1961b), in forthcoming investigations.

Cohl, H. S., J. E. Tohline, A. R. P. Rau, H. M. Srivastava (2000)

Astronomische Nachrichten, 321, 5/6, 363-372.

"Developments in determining the gravitational potential using toroidal functions."

Site at a Glance: