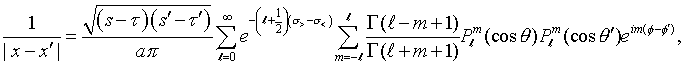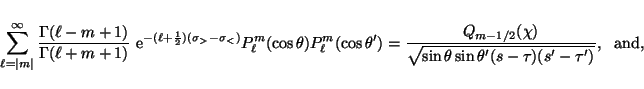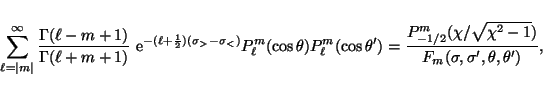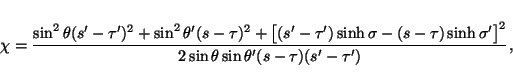Next: Toroidal Coordinates
Up: Two Fourth-Order Rotational Laplace
Previous: Two Fourth-Order Rotational Laplace
CLICK TEXT TO READ PDF COPY OF PAPER
In bispherical coordinates --
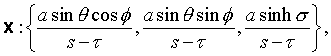 where
where
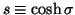 goes from 1 to
goes from 1 to 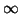 ,
,
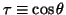 goes from -1 to +1, and
goes from -1 to +1, and
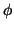 goes from 0 to
goes from 0 to 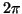 -- the
surfaces
-- the
surfaces 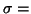 constant are spheres and the surface
constant are spheres and the surface 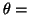 constant is a spindle-shaped cyclide. According to eq. (10.3.74) of
Morse & Feshbach (1953),
constant is a spindle-shaped cyclide. According to eq. (10.3.74) of
Morse & Feshbach (1953),
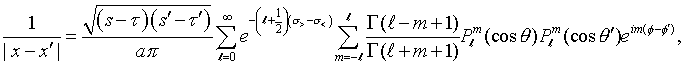
|
(44) |
Consequently, the following two expressions must be valid
addition theorems:
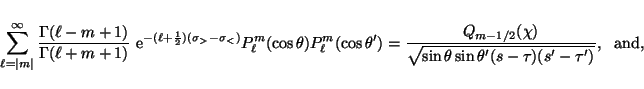 |
(45) |
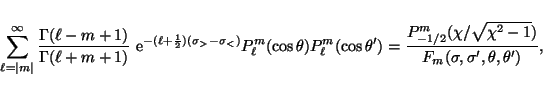 |
(46) |
where
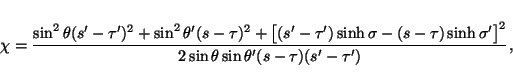 |
(47) |
and
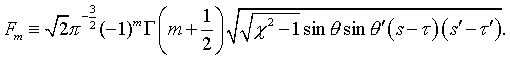
Howard S. Cohl
2000-10-05
Cohl, H. S., J. E. Tohline, A. R. P. Rau, H. M. Srivastava (2000)
Site at a Glance: