CLICK TEXT TO READ PDF COPY OF PAPER
The circular cylindrical coordinate system is unique in that it is the only
coordinate system that is known to be separable for Laplace's
equation as well as being a member of both the rotational and cylindrical
classes. In cylindrical coordinates --
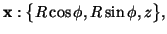 where the radial coordinate R goes from 0 to
where the radial coordinate R goes from 0 to  the azimuthal coordinate
the azimuthal coordinate 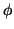 goes from 0 to
goes from 0 to 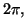 and the vertical coordinate z goes from
and the vertical coordinate z goes from 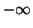 to
to 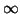 -- the reciprocal distance between two points
-- the reciprocal distance between two points 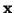 and
and
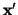 can be given in many different forms. For instance, here
we write the Green's function for Laplace's equation in terms of
the integral of Lipschitz (see prob. 3.14 in Jackson 1975 or
§13.2 in Watson 1944),
can be given in many different forms. For instance, here
we write the Green's function for Laplace's equation in terms of
the integral of Lipschitz (see prob. 3.14 in Jackson 1975 or
§13.2 in Watson 1944),
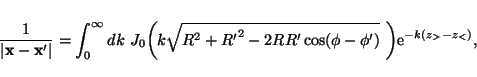 |
(8) |
where J0 is the order zero Bessel function of the first kind. Alternatively, this same quantity can be written in a form of the Lipschitz-Hankel integral (§3.11 in Jackson 1975; §13.21 in Watson 1944),
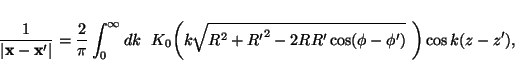 |
(9) |
where K0 is the order zero modified Bessel function of the second kind. According to Neumann's addition theorem for Bessel functions, the order zero Bessel function of the first kind can be written as a Fourier series expansion over products of Bessel functions of varying order, namely (§11.1 in Watson 1944),
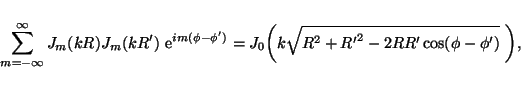 |
(10) |
where Jm is the order m Bessel function of the first kind. In the same vein, the order zero modified Bessel function of the second kind can be expanded as follows using Graf's generalization of Neumann's addition theorem (§11.3 in Watson 1944):
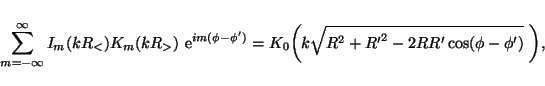 |
(11) |
where Im and Km are the order m modified Bessel functions of the first and second kind, respectively. Substituting the two addition theorems (10) and (11) into the integral expressions (8) and (9), respectively, yields the following two double integration/summation expressions for the Green's function (problem 3.14 of Jackson 1975)
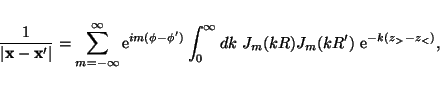 |
(12) |
and (§3.11 of Jackson 1975),
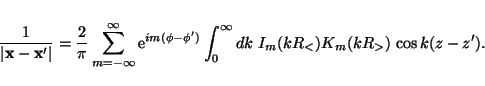 |
(13) |
We can further simplify both of these double summation/integration expressions through the use of known transcendental function solutions to the integrals in both (12) and (13) as given, for example, by eq. (13.22.2) in Watson (1944) and eq. (6.672.4) in Gradshteyn & Ryzhik (1994), namely,
![\begin{displaymath}\int_{0}^{\infty}\ dk
\ J_m(kR)J_m(kR^\prime)
\ \mathrm{e}^...
...ggl[\frac{R^2+{R^\prime}^2+(z-z^\prime)^2}{2RR^\prime}\biggr],
\end{displaymath}](img37.gif) |
(14) |
and,
![\begin{displaymath}\int_{0}^{\infty} dk
\ I_m(kR_<) K_m(kR_>)
\cos k(z-z^\prime...
...ggl[\frac{R^2+{R^\prime}^2+(z-z^\prime)^2}{2RR^\prime}\biggr],
\end{displaymath}](img38.gif) |
(15) |
where
![]() is the odd-half-integer
degree Legendre function of the second kind. Hence, we may rewrite
both eqs. (12) and (13) in the following compact azimuthal Fourier
series form:
is the odd-half-integer
degree Legendre function of the second kind. Hence, we may rewrite
both eqs. (12) and (13) in the following compact azimuthal Fourier
series form:
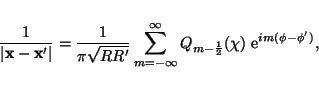 |
(16) |
where
 |
(17) |
Equation (16) is the Green's function expansion that was presented in Cohl & Tohline (1999) as an alternative to the standard multipole expansion technique.
In fact, this result can be easily derived by starting with the algebraic expression for the Green's function in cylindrical coordinates,
![\begin{displaymath}\frac{1}{\vert{\bf x} - {\bf x^\prime}\vert}=
\frac{1}{\sqrt{...
...}{2RR^\prime}
-\cos(\phi-\phi^\prime)\ \biggr]^{-\frac{1}{2}},
\end{displaymath}](img42.gif) |
(18) |
and using the Heine identity (§10.2 in Bateman 1959; §74 in Heine 1881; see also §4.5.4 of Magnus, Oberhettinger, and Soni 1966),
![\begin{displaymath}\sum_{n=-\infty}^\infty
Q_{n-\frac{1}{2}}(s)
\ \mathrm{e}^{i...
...i}=
\ \!\pi\bigl[\ \!\!2\ \!(s-\tau)\ \!\bigr]^{-\frac{1}{2}},
\end{displaymath}](img43.gif) |
(19) |
where
![]() and
and
![]() Using (19) to expand (18) immediately yields (16).
Using (19) to expand (18) immediately yields (16).
Although the use of Heine's identity leads to the main result (16) more quickly, addition theorems such as (10) and (11) can be extremely useful when casting various expressions for the Green's function for Laplace's equation in different coordinate systems in terms of single summation/integration expressions like (8), (9), and (16). Such expressions encapsulate the symmetries manifested within these diverse forms. In what follows we offer an interesting twist on the development in the theory of addition theorems. We note that the essential ingredient which leads to our new development, eq. (19), was given by Heine (1881) over a century ago in, ``Handbuch der Kugelfunctionen,''1* but it appears not to have been utilized much in practical astrophysics applications over the past century.
1Richard Askey, general editor for the section on special functions in the "Encyclopedia of Mathematics and its Applications" in his foreword to Miller (1977) says, in regard to the addition theorem for spherical harmonics and the corresponding addition theorem for trigonometric functions, "...(these) are among the most important facts known about these functions." Whittaker and Watson (1943) further expound on the addition theorems in Chapter XV on Legendre functions. Watson (1944) devotes his chapter XI to the discussion the addition theorems known then for Bessel functions. Hobson (1931) devotes his chapter VIII to the discussion of the addition theorems known then for associated Legendre functions. Hobson (1931) proclaims of Heine's "Inaugural dissertation ... which has hitherto been the only treatise dealing with the functions which could claim to be complete ...," and in connection with Eduard Heine " ... he first introduced the Legendre's function of the second kind, together with the associated functions."
* Note added by H.S. Cohl on December 5, 2002: The title of Heinrich Eduard Heine's inaugural dissertation is *not* "Handbuch der Kugelfunktionen." The correct spelling of the title of his book is "Handbuch der Kugelfunctionen." In the version of this paper which appears in Astronomische Nachrichten, this misspelled version of the paper appears. The fault lies in several interesting mis-quotations of the title of his book, such as which appear in Whittaker and Watson (1927) on page 316, as well as in Hobson's (1931) treatise. I have a copy of Heine's book and the title is indeed "Handbuch der Kugelfunctionen." It seems as though Heine was one of the first to coin the term "function," spelled with a "c". I am not aware of any copies of Heine's text where he uses the "k". However is is hard to believe that Whittaker and Watson (1927) made a serious blunder like this. In fact, on page 330, Whittaker and Watson (1927) mentions a reference by L. Schläfli "Ueber die zwei Heine'schen Kugelfunktionen" (Bern, 1881). Again with the "k"! If anyone knows what is going on here, please let me know.
Next: The Highly Symmetric Nature Up: Developments in Determining the Previous: Rotationally Invariant Coordinate Systems