"Parallel Implementation of a Data-Transpose Technique for the Solution of Poisson's Equation in Cylindrical Coordinates"
Proceedings of the 8th SIAM Conference on Parallel Processing for Scientific Computing, Minneapolis, Minnesota, March.
1999a - Cohl, H. S.
"On the numerical solution of the cylindrical Poisson equation for isolated self-gravitating systems"
The Louisiana State University and Agricultural and Mechanical College, 122 pages
1999b - Cohl, H. S. and J. E. Tohline
"A Compact Cylindrical Green's Function Expansion for the Solution of Potential Problems"
The Astrophysical Journal, 527, 86-101.
2000 - Cohl, H. S., J. E. Tohline, A. R. P. Rau, H. M. Srivastava
"Developments in determining the gravitational potential using toroidal functions"
Astronomische Nachrichten, 321, 5/6, 363-372.
2001 - Cohl, H. S., Rau, A. R. P., Tohline, J. E., Browne, D. A., Cazes, J. E. and Barnes, E. I.
"Useful alternative to the multipole expansion of 1/r potentials"
Physical Review A: Atomic and Molecular Physics and Dynamics, 64, 5, 52509.
2002 - Cohl, H. S.
"Portent of Heine's Reciprocal Square Root Identity"
Proceedings of the 3D Stellar Evolution Workshop, ed. R. Cavallo, S. Keller, S. Turcotte, Livermore, California
- ...
equation.
![[*]](/home/hcohl/LaTeX2HTML/latex2html/icons.gif/foot_motif.gif)
- This paper, in a modified form, was presented in a poster
format at the 200th IAU symposium on binary star formation (held in
Potsdam, Germany April 10-15, 2000).
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
- ... Kugelfunctionen,''
![[*]](/home/hcohl/LaTeX2HTML/latex2html/icons.gif/foot_motif.gif)
-
Richard Askey, general editor for the section on special functions in the
``Encyclopedia of Mathematics and it's Applications,'' in his forward to
Miller (1977) says, in regard to the addition theorem for spherical
harmonics and the corresponding addition theorem for trigonometric
functions, ``... (these) are among the most important facts known about
these functions.'' Whittaker and Watson (1943) further expound on the
addition theorems in chapter XV on Legendre functions.
Watson (1944) devotes his chapter XI to the discussion of the
addition theorems known then for Bessel functions.
Hobson (1931) devotes his chapter VIII to the discussion of the addition theorems known then for associated Legendre functions.
Hobson (1931) proclaims of Heine's ``Inaugural dissertation...which has
hitherto been the only treatise dealing with the functions
which could claim to be complete...'' and in connection with Eduard
Heine,``...he first introduced the Legendre's functions of the second kind,
together with the associated functions.''
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
- ... derive,
![[*]](/home/hcohl/LaTeX2HTML/latex2html/icons.gif/foot_motif.gif)
-
Once the main result (16) was derived, the solution's form in terms of
toroidal functions suggested that the Green's function in toroidal
coordinates should be examined with care. In so doing we have noticed that
there is a typographical error in eq. (10.3.81) in Morse & Feshbach's
(1953) expression of the Gamma functions in their double summation
Green's function expansion in toroidal coordinates (10.3.81). The
appearance of integer powers of i in Morse & Feshbach's presentation
of the double summation expressions in prolate spheroidal coordinates
(10.3.53), oblate spheroidal coordinates (10.3.63), and toroidal
coordinates (10.3.81) is not understood. This seemingly inaccurate
trait of associated Legendre functions is further demonstrated in their
numerical tables VII, VIII, and IX of the associated Legendre functions
at the end of Part II of their series. There is also an error in their
accounting of Heine's identity, eq. (19), in two separate locations;
eq. (10.3.79) and the last equation that appears in their chap. 10.
In both locations, the Neumann factor
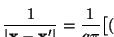 is missing. The Neumann factor is a natural consequence of going from
a complex exponential notation (Fourier series) to a cosine representation
(purely real) of a series. If Morse & Feshbach (1953) had noticed these
minor errors in their presentation, the results presented in this paper
would most likely have already been completely established.
is missing. The Neumann factor is a natural consequence of going from
a complex exponential notation (Fourier series) to a cosine representation
(purely real) of a series. If Morse & Feshbach (1953) had noticed these
minor errors in their presentation, the results presented in this paper
would most likely have already been completely established.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2000-10-05