Given an arbitrary real function of 3 space variables, the integral over the entire
domain can be given simply by the integral of the m=0 axisymmetric Fourier component
of that function over the entire half-plane given by ( R >= 0 , - infinity <= z <= infinity ).

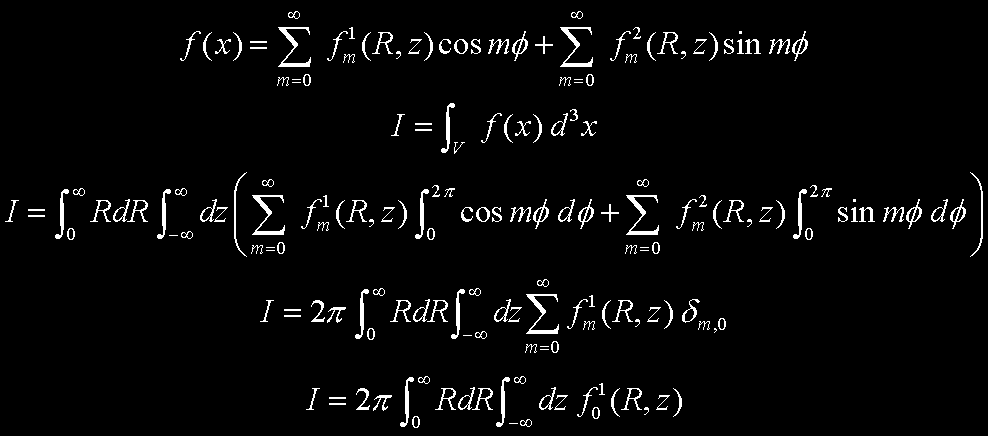
The Axisymmetry Mass/Charge Self-Energy Equivalence Theorem

Theorem:

Given any arbitrarily chosen set of orthogonal Cartesian axes, the classical potential
gravitational/electrostatic self-energy of a fully non-axisymmetric mass/charge density
distribution will be precisely given by an equivalent arbitrarily oriented, azimuthally
averaged, axisymmetric mass/charge density distribution.

Single Point Single Loop corollary

The potential self-energy of a mass/charge loop has the same self-energy as a point
mass/charge isolated arbitrarily anywhere along that loop with the same total
mass/charge of the loop.



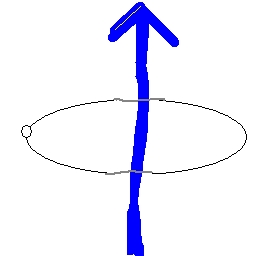
Single Point Single Sphere corollary

The potential self-energy of a mass/charge spherical shell has the same self-energy as a point
mass/charge isolated arbitrarily anywhere on the surface of the shell with same total
mass/charge of the point.



Double Point Double Loop corollary

Two mass/charge points have equivalent self-energy of two loops which pass through each of the
points each having he same total mass/charge forming a two loops around any axis of choice.



Double Point Single Loop corollary

Two mass/charge points have equivalent self-energy of a single loop which passes
through each of the two point mass/charges having he total mass/charge of the
sum of the two point masses/charges with axes chosen to orient vertically at any
angle in the equatorial plane.

and therefore...



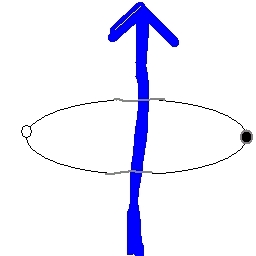
Double Point Double Sphere corollary

If the arbitrary axis of symmetry is chosen to lie along the line which
doesn't connect the two mass/charge points then the self-energy configuration
of those two points is energetically equivalent to the combination of two
infinitesimally thin spherical shells with diameter equal to twice the
separation distances from the origin corresponding to each of the two
point mass/charges with total mass/charge of each spherical shell equal
to the total mass/charge of each corresponding point.







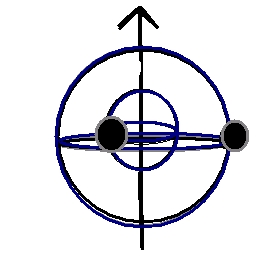
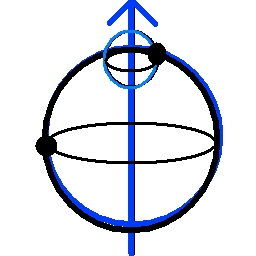
Double Point Single Sphere corollary

If the arbitrary axis of symmetry is chosen to lie along the line which connects
the two mass/charge points then the self-energy configuration of those two points is
energetically equivalent to an infinitesimally thin spherical shell with diameter
equal to the separation distance of the two point mass/charges with total
mass/charge equal to the sum of the two point masses/charges.



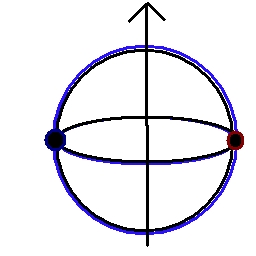
Bullseye Single Lifted or Lowered Loop and Point corollary

If the axis is chosen to lie non-orthogonally to the position vector from the
first point mass/charge to a second point mass/charge, then the self-energy of this
configuration is equivalent to a loop vertically lifted or lowered from the second
point mass/charge.





Bullseye Single Loop and Single Point Corollary
If the axis of symmetry is chosen to point towards any orthogonal direction from
one point mass/charge to another, then the self-energy configuration is energetically
equivalent to a point mass/charge with a circular loop centered on it with total
mass/charge equal to the second point.

Proof:

The gravitational classical potential self-energy is given by the following double
integral over the primed and unprimed coordinates and over all space is given



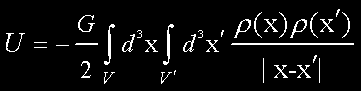
Now we introduce an azimuthal Fourier series expansion of the azimuthal eigenmodes
of the density and potential



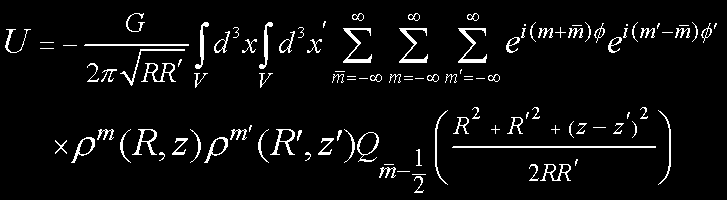
The terms of this series are invariant under the change m->-m. So therefore
the self-energy in terms of real values and nonnegative m's is



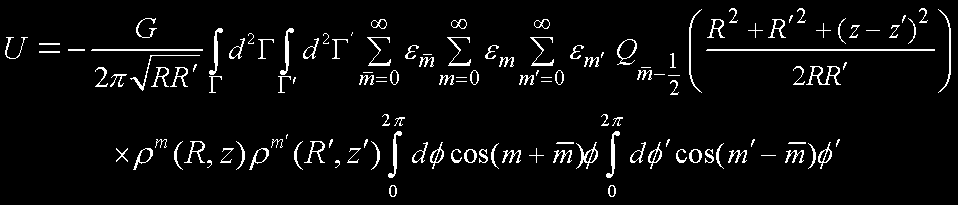
is called the Neumann factor which always appears when using
only positive m values.

Only the m=0 term in the self-energy survives



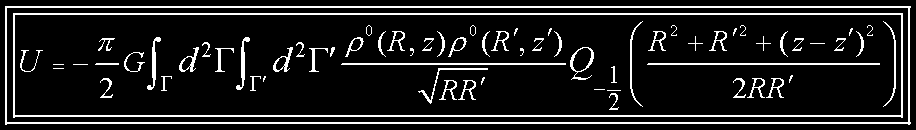
which can be rewritten in terms of the complete elliptic integral of the

!

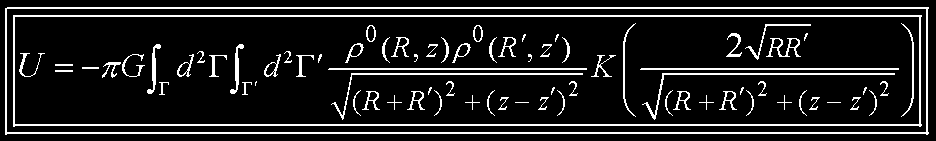next page