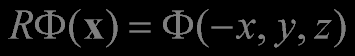Symmetry in Laplace's Equation
The known coordinate systems that permit separation
of variables for Laplace's equation were given in the classic text by
Maxime Bôcher (1894)
"Die Reihenentwickelungen
der Potentialtheorie"
Precise description of symmetries within Laplace's
equation through Lie theory is given in Willard Miller (1977) "Symmetry and Separation of Variables"
-Lie Theory-
Apart from the trivial symmetry E through time-invariance. The symmetry algebra of Laplace's equation is 10 dimensional with basis given by
Linear Momentum Operators
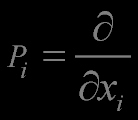
Dilatation Operator
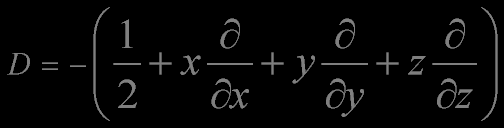
Angular Momentum Operator
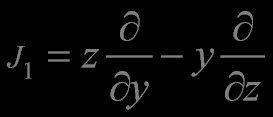
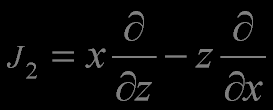
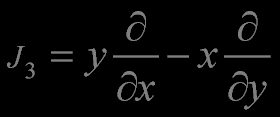
The generators of special conformal transformations
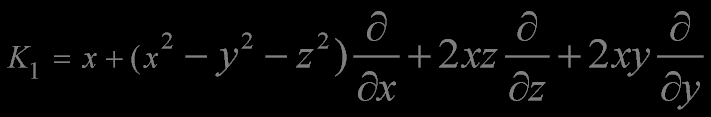
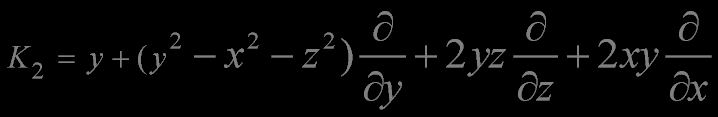
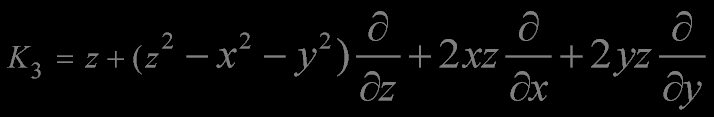
The linear and angular momentum operators generate a subalgebra isomorphic
to
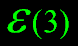and D is the generators of dilitations
the operator K is the generator of special conformal transformations
The symmetry algebra of Laplace's equation is isomorphic to so(4,1)
the Lie algebra of all real 5x5 matrices
such that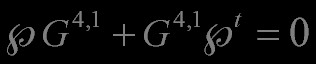
where
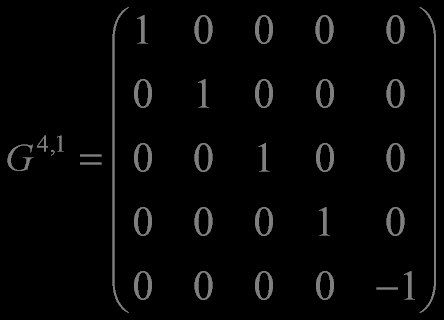
The dilatation operator generates
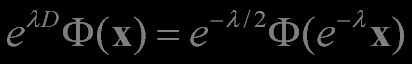
The generator of special conformal transformations generates
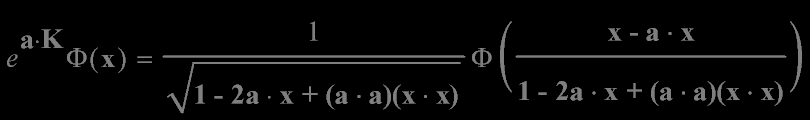
There are two additional well-known symmetries of Laplace's equation which are not generated by the above operators
The inversion operator
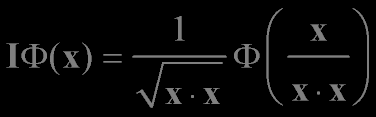
The reflection operator
