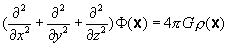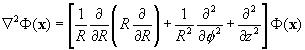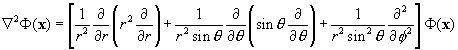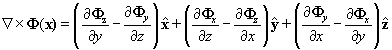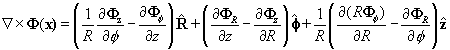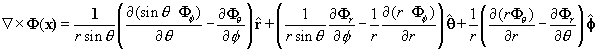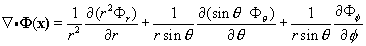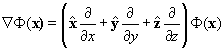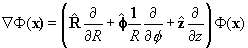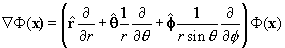"Parallel Implementation of a Data-Transpose Technique for the Solution of Poisson's Equation in Cylindrical Coordinates"
Proceedings of the 8th SIAM Conference on Parallel Processing for Scientific Computing, Minneapolis, Minnesota, March.
1999a - Cohl, H. S.
"On the numerical solution of the cylindrical Poisson equation for isolated self-gravitating systems"
The Louisiana State University and Agricultural and Mechanical College, 122 pages
1999b - Cohl, H. S. and J. E. Tohline
"A Compact Cylindrical Green's Function Expansion for the Solution of Potential Problems"
The Astrophysical Journal, 527, 86-101.
2000 - Cohl, H. S., J. E. Tohline, A. R. P. Rau, H. M. Srivastava
"Developments in determining the gravitational potential using toroidal functions"
Astronomische Nachrichten, 321, 5/6, 363-372.
2001 - Cohl, H. S., Rau, A. R. P., Tohline, J. E., Browne, D. A., Cazes, J. E. and Barnes, E. I.
"Useful alternative to the multipole expansion of 1/r potentials"
Physical Review A: Atomic and Molecular Physics and Dynamics, 64, 5, 52509.
2002 - Cohl, H. S.
"Portent of Heine's Reciprocal Square Root Identity"
Proceedings of the 3D Stellar Evolution Workshop, ed. R. Cavallo, S. Keller, S. Turcotte, Livermore, California
The Harmonics The:
Separable Analytical Solutions to
Separable Analytical Solutions to
Laplace's Equation
The Quadrics and the
Cyclides (Howard S. Cohl) 7/28/01
Those smooth Transcendental Functions,
the 3D Harmonic Functions, the Harmonics (Howard S. Cohl) 7/23/01
Elementary functions:
Exponential functions and Logarithmic functions:
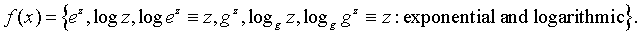
Solutions to the differential equation and it's inverse:
Trigonometric functions (six kinds of solutions to the differential
equation and their inverses)
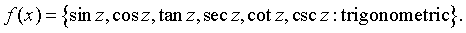
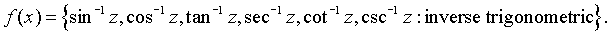
Hyperbolic functions (six kinds of solutions to the differential equation
and their inverses)
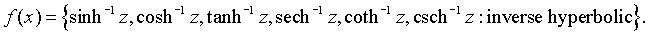
Jacobi Elliptic functions (twelve kinds of solutions to the differential equation
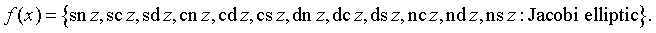
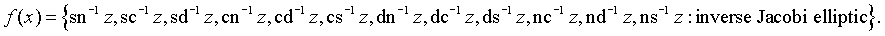
Many kinds of solutions to the differential equation and their inverses
Elliptic Integrals
two kinds of solutions to the differential equation
Gamma functions
one kind of solution to the differential equation
Bessel functions
two kinds, two kinds, and two kinds of solutions to the differential equation
Lame' functions
two kinds of solutions to the differential equations
Dirac Delta functions
one kind, or rather ... (no differential equation, it's a different type
of function than we ordinarily used to dealing with, but extremely
important in mathematical physics)
Legendre functions
The Legendre Differential Equation:
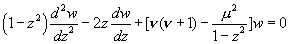
two kinds of solutions to the differential equations, (and their inverses?, ...more later on that coming)
;
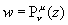nu is called the degree, mu is called the order, and z is the argument.
with general complex nu, mu and z. Serious! These functions remain almost completely unexplored
plus they have extremely beautiful properties. I know beauty is in the eye of he beholder, but
the beauty inherent in Legendre functions is geometrical in nature. We all know about the conic
sections, for instance. Circles, ellipses, hyperbolae, parabolas, one or two lines, line segments
and rays with their various limits, did I forget any? Well, in fact, these conic sections generalize
most effective in a three dimensional space, that is, Legendre functions alone seem to be critical
in the development of spheres, oblate and prolate spheroids, tori, hyperboloids of revolution
of one and two sheets, cones, bispheres of revolution, and spindle-shaped cyclides, and spherical
bowls. We are going to display these geometries in a most beautiful fashion. These functions are
all rotational invariant, that is, if we rotate these figures, they don't change in appearance.
The other transcendental functions which have this same property are Bessel functions, they generate
cylinders and paraboloids of revolution. See the chapter on Bessel functions. When I first started
out I was a lot more interested in Bessel functions than Legendre functions, but now Legendre
functions are my favorite, and I will continue to explain why.
Gauss Hypergeometric Legendre P Expressions:
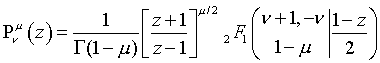
(|1-z|<2)
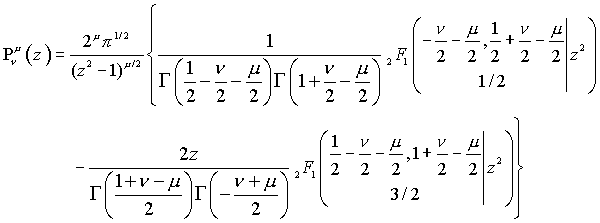(|z^2|<1)
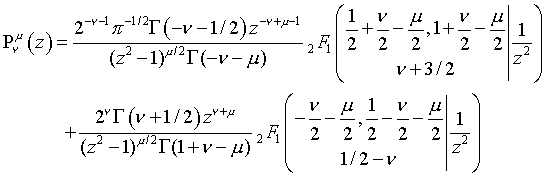(|1/z^2|<1)
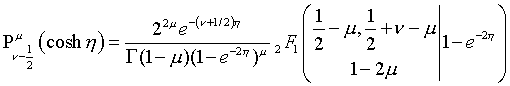(cosh eta>1)
Gauss Hypergeometric Legendre Q Expressions:
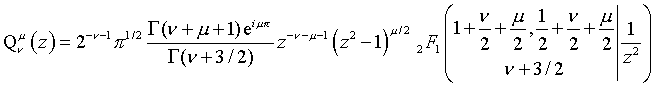(|z|>1)
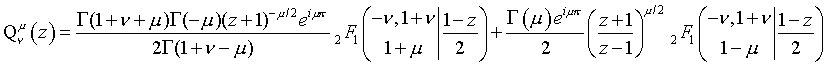(|1-z|<2)
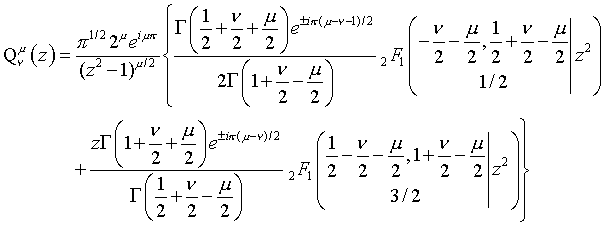(|z^2|<1)
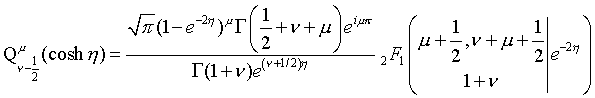(cosh eta>1)
Complex arguments
Real arguments from -1 to 1: trigonometric arguments.
Real arguments from 1 to infinity: hyperbolic arguments.
Purely imaginary arguments from i*0 to i*infinity: hyperbolic arguments.
2he relations between the orders and the degrees.
Complex orders and complex degrees.
Integer orders and integer degrees.
Integer orders and odd-half-integer degrees.
Odd-half-integer orders and integer degrees.
Odd-half-integer orders and odd-half-integer degrees.
Assorted other rational orders and degrees.
Toroidal functions
- Introduction
- Rotationally Invariant Coordinate Systems which Separate Laplace's Equation
- The Rotational Cylindrical System
- The Highly Symmetric Nature of Toroidal Functions
- Three Second-Order Rotational Laplace Systems
- Two Fourth-Order Rotational Laplace Systems
- Conclusion
- Bibliography
- About this document ...
WHIPPLE FORMULAE
7/22/01 - The Whipple Formulae for Toroidal Functions (H.S. Cohl)
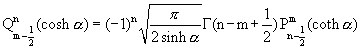
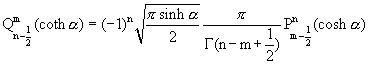
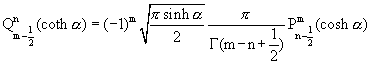
OK! This is one of the first basic entries. Let's all start thinking about this
if you have any ideas, corrections, misconceptions, or comments in general,
I will glad to hear what you have to say, if your even a slight bit interested
in this, I would be glad to hear. Check out some of my ideas about the
Whipple formulae as they are applied to toroidal or ring functions. These
Whipple formulae have been presented previously in terms of a viewpoint
aimed at spherical harmonics, now that we view the equations in terms
of toroidal coordinates, whole new symmetries of Legendre functions arise.
Well, these interesting functions have the properties that they can relate
Legendre functions of the first and second kinds directly in terms of each
other. The only hitch is that you need a different argument to relate them.
The way it works it as such. The Legendre functions of the first kind generally
are well-behaved near the origin and blow up at positive infinity. Consequently
the Legendre functions of the second kind blow up at unity and exponentially
converges towards zero for large values of the argument. The relevant domain
for toroidal functions is from 1 to infinity. The standard hyperbolic argument
for these functions are naturally chosen to be the hyperbolic cosine since it
ranges from 1 to infinity. The Whipple formulae relate the Legendre functions
with argument 1 to infinity, cosh, to a reversed range given by the hyperbolic
cotangent function. the hyperbolic cotangent function ranges from infinity at
unity to unity at infinity.
At what point alpha does cosh alpha equal coth alpha? The point alpha is given by
.
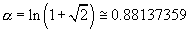Therefore, exp(alpha) and exp(-alpha) are respectively given by
,
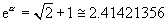and
.
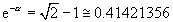The value that cosh alpha and coth alpha obtain at alpha is given by
.
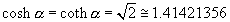The value that sech alpha and tanh alpha obtain at alpha is given by
.
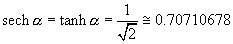Finally, sinh alpha and it's inverse csch alpha are given respectively by unity
.
We now see that the value at which the argument of the Legendre functions inversely
maps the entire domain is given by cosh alpha = coth alpha ~ 1.4142356. By
using the Whipple formulae for ring functions, we can inversely map the entire
domain from 1 to infinity about this point cosh alpha, the square root of 2, and
take full advantage of this new symmetry for Legendre functions. There being
previously more definite and indefinite integrals tabulated for the Legendre function
of the first kind than for the Legendre function of the second kind. In fact, this
new transformation, when applied to toroidal functions yields distinct expressions
which relate correspondingly the complete elliptic integrals of the first and second
kind, which don't seem to be related to the linear and quadratic transformations of
hypergeometric functions.
Spherical harmonics
Conical harmonics
Oblate spheroidal harmonics
Prolate spheroidal harmonics
Bispherical harmonics
Site: H.S. Cohl 7/22/01 - The Potential of a Point : Laplace's equation
CHAPTER I: Symmetry in PDEs
CHAPTER II: Laplace's equation
CHAPTER III: Poisson's equation
CHAPTER IV: The quadrics and the cylcides
CHAPTER V: Symmetric classes
III.A : Translational class:
III.B : Rotational class:
III.C : Corporeal class:
BASIC TO COMPLEX WE REACH ALL LEVELS HOPEFULLY, ... eventually for sure. he he
INTRODUCTION: Symmetry in PDEs
Studies of the Solution of Laplace's equation and Poisson's
equation.
Recent investigations pose questions regarding the form
of known available analytic solutions of Laplace's equation.
The technique of separation of variables has been
widely employed in order to study the form and behavior of
solutions to various partial differential equations.
Furthermore there exists solutions to Laplace's equation
which can be obtained using R-separation of varibales (R).
Geometrical representations of these solutions cast them
in the light of orthogonal curvilear coordinate systems.
In the 9 coordinate systems whose solution to Laplace's
equation can be obtained through the standard separation
of variables (S) technique the family of surfaces obtained
are quadrics. The "bonus" solutions which can be derived
through R lead to solutions which are families of cyclides.
Recent studies of the analytic form of the infinite extent
Green's function for Laplace's equation sheds new light on
the reasons for the existance of R type solutions. These
systems which can be obtained for coordinate systems which
are axisymmetric and have known analytic solutions to
Laplace's equation through separations of variables, exhibit
a new symmetry in terms of the azimuthal Fourier components
of their solutions.
Laplace's equation is:
Poisson's equation (as applied to Newtonian gravity) is:
where both \Phi and \rho are functions of all three
Cartesian variables and del^2 is the Laplacian operator
defined in terms of Cartesian coordinates (rectangular)
as follows:
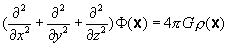
The Laplacian del^2=d/dx^2 + d/dy^2 + d/dz^2 is an
operator which is found all over the place whenever
people try to describe physical systems with
mathematics (This discipline is called Mathematical physics).
It appears in eq. (1), Poisson's equation, the heat equation,
the diffusion equations, Helmholtz's equation, the Schroedinger
equation, plus more ... Very important operator.
Something interesting to think about. Remember the
fundamental equation of Green's functions
The Green's function ion any coordinate system must satisfy
this equation. What does it mean? Well, the solution of
any potential problem satisfies Poisson's equation, eq. (2).
That is, given a source of density, \rho, it will introduce an
field (either Electric or Gravitational), into space which
can be obtained by determining the gradient of a potential
function \Phi throughout all space. That is where \rho is
zero (empty space) Poisson's equation works (in empty space
Poisson's equation with \rho = 0 is Laplace's equation).
And within the matter, where \rho is not zero, Poisson's
equation also works. So the inhomogeneous equation (Poisson's
equation) is more general that Laplace's equation.) But
solutions to Laplace's equation are very easy to obtain
using the separation variables technique for a certain class
of coordinate system which have been tabulated to death
since they were first discovered in the 1800's or earlier even.
So there is a wealth of information on analytic (pen and paper)
solutions to Laplace's equation. This is good for us.
The analytic method for Poisson's equation is called the Green's
function method. It is an integral method. That is, the solution
of the differential equation is given by an integral equation.
This is an equation very similar to a differential equation
but it contains integrals as well as derivatives. Hard to solve.
But the boundary conditions are built right in. One then needs
the potential boundary values on a cylindrical boundary, in order
to solve Poisson's equation.
Eq. (4) contains a Dirac delta function. Dirac was the first
mathematician/physicist who worked seriously with these types
of functions. Actually in a strict mathematical sense,
the Dirac delta function (which I will from here on refer to
as Delta function) isn't a function. We can go into that
more later if you are interested. Dirac used the delta function
to describe the density of an electron, as a point source.
It gives the right answer, which you can convince yourself of.
The three-dimensional delta function is zero everywhere, except
at xvec=xvec^\prime, there it is infinity, and if you integrate
the three dimensional delta function over space volume*density
gives you the mass (or charge) of the point source. Now, since
we can approximate ANY mass (charge) distribution
as a continuous collection of point masses (charges) we can
integrate over all point sources (\rho) in order to obtain the
Potential everywhere. This is just as good mathematically
as solving Poisson's equation given the boundary conditions.
This is why the Dirac delta function appears in the derivation of
Green's functions. So, we must understand how we calculate the
delta function is all of our so called "interesting" coordinate
systems. Jackson (1977) gives a very nice explanation of how this is
done.
Elementary functions are absolutely crucial, and
transcendental functions
lead us through a realm of mathematical possibilities that we had
not even considered before.
CHAPTER II: Laplace's equation
CHAPTER III: Poisson's equation
CHAPTER IV: The quadrics and the cylcides
CHAPTER V: Symmetric classes
III.A : Translational class:
III.B : Rotational class:
III.C : Corporeal class:
The Laplacians,Curls,
Divergences, Gradients,
and Elements:
The Laplacians: Here we attempt to give you the Laplacians in
various coordinate systems.
Cartesian coordinates
Cylindrical coordinates
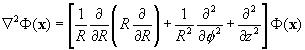
Spherical coordinates
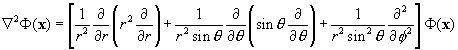
The Curls: Here we attempt to give you the Curls in
various coordinate systems.
Cartesian coordinates
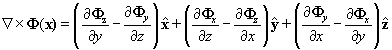
Cylindrical coordinates
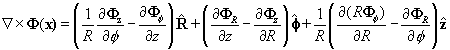
Spherical coordinates
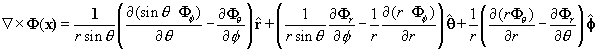
The Divergences: Here we attempt to give you the Divergences in
various coordinate systems.
Cartesian coordinates
Cylindrical coordinates
Spherical coordinates
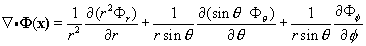
The Gradients : Here we attempt to give you the Gradient in
various coordinate systems.
Cartesian coordinates
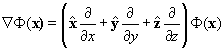
Cylindrical coordinates
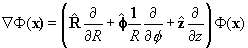
Spherical coordinates
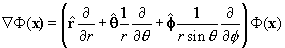
The Elements: Here we attempt to give you the line, area,
and volume elements in various coordinate systems.
Cartesian coordinates
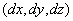
Cylindrical coordinates
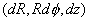
Spherical coordinates
If you have any ideas, corrections, misconceptions, or comments in general,
I will glad to hear what you have to say. If your even a slight bit
interested in this, I would be glad to hear from you. Check out some of my
ideas about the Whipple formulae as they are applied to toroidal or ring
functions. These Whipple formulae have been presented previously in terms
of a viewpoint aimed at spherical harmonics, now that we view the equations
in terms of toroidal coordinates, whole new symmetries of Legendre functions
arise.
Some of the most amazing and interesting things that we can explore
in our world is math. Some other things which interest us are
in nature. We love the clouds, the skies, the plants, and the animals.
There is a lot of beauty in the universe. When observational
astronomers observe the celestial sphere, they witness an even greater
diversity than we witness here on the earth. Here on the outskirts of
the milky way, we are quite content but curious nonetheless.
Being an astronomer, like Newton or Kepler must have been quite exciting.
I am sure they enjoyed their work with the satisfaction that comes along
with discovery. Nowadays the Universe is constantly being observed and
many puzzles arise and have arisen which are difficult to explain.
Modern theoretical astrophysicists must work diligently in their
efforts to explain the way things work. Still we must persevere,
and search where no one has searched before to find answers to these
questions. Remember, further generalizations usually exist.
You might as ask what transcendental functions have to do with all of this?
;
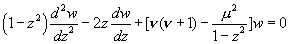
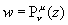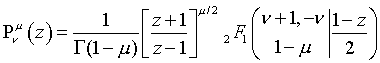
(|1-z|<2) 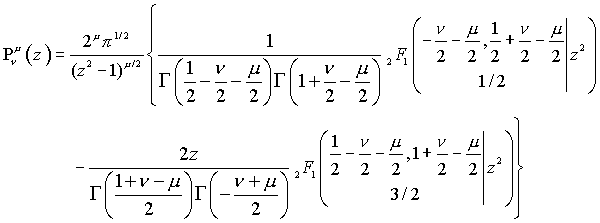(|z^2|<1) 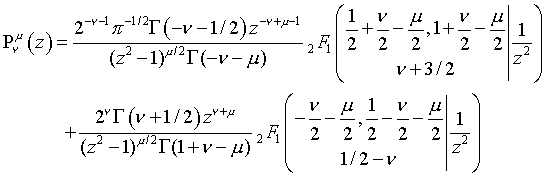(|1/z^2|<1) 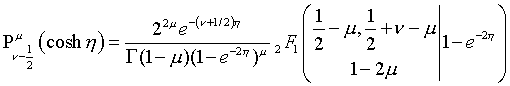(cosh eta>1) 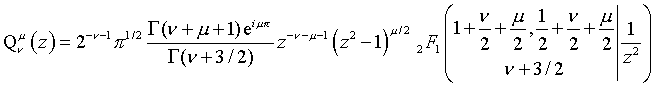(|z|>1) 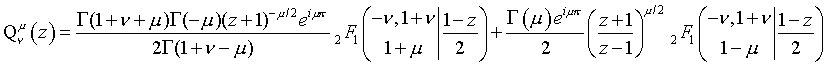(|1-z|<2) 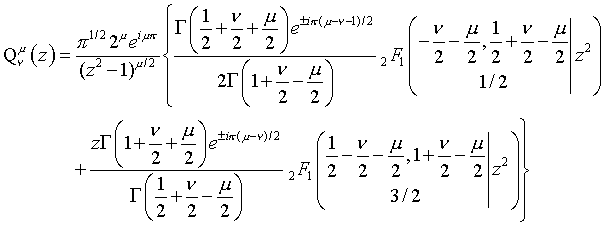(|z^2|<1) 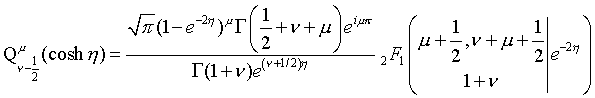(cosh eta>1)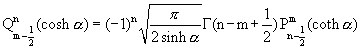
. , . . . .
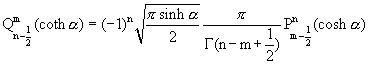
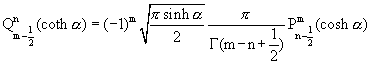
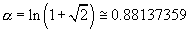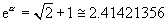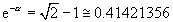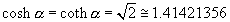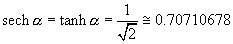